Top-Level Pippenger Design

Pippenger’s Algorithm

The main idea of Pippenger’s algorithm is to reformulate the dot products $∑↙{i=0}↖{N-1} p_{i} s_{i}$ into smaller dot products over windows, where every window represents a small contiguous set of bits from the scalar:

$p_{i}$ and $s_{i}$ are elements of the prime field and scalar fields respectively, and the product $BW$ must be greater or equal to the number of bits of the scalar field.

The inner sum in parentheses is computed using the bucket method depicted by the following Python pseudocode:

B : int = .. # log size of buckets, This is a tunable parameter.
identity = ...  # A special point such that P + identity = identity + P = P

def bucket_aggregation(scalars, points):
  buckets = [ identity for p in range(2**B) ]
  for scalar, point in zip(scalars, points):
    buckets[scalar] += point
  return buckets

def bucket_sum(bucket):
  acc = identity
  running = identity
  for point in reversed(points):
    running += point
    acc += running
  return acc

def bucket_method(scalars, points):
  return bucket_sum(bucket_aggregation(scalars, points))

Overview of the Architecture

In the specific case of BLS12-377, the prime field and scalar field are 377 bits and 253 bits respectively. In our implementation, we have partitioned the work such that the FPGA performs the bucket aggregation and the host performs the final bucket sum. When processing multiple MSMs, this allows us to mask out the latency of bucket sum by starting the bucket aggregation of the next MSM while computing bucket sum for the current MSM.

Considerations for the choice of parameters $B$ and $W$ are:

• The amount of on-chip memory resources available in the FPGA
• The amount of time taken to perform the bucket sum on the host

We have chosen $B=13$ and $W=20$ in our implementation, as this uses up ~60% of the memory resources available and the time taken for bucket sum is around 1/10th the time taken for bucket aggregation. This allows our implementation to have a comfortable margin for routing in the FPGA and for the bucket sum to be fast enough relative to bucket aggregation. We discuss some ideas on improving the performance further in the future work section.

FPGA Dataflow

Here’s a high level block diagram showing the different data flows and modules used in our MSM implementation.

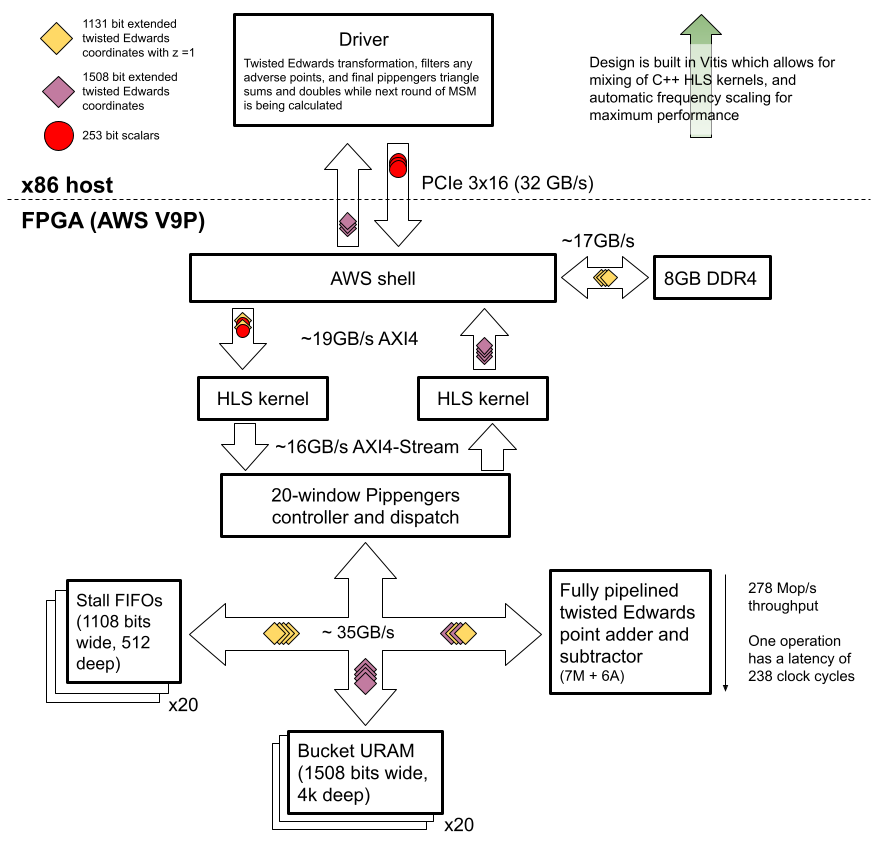
Points are transformed into a custom representation and pre-loaded into DDR-4, so that at run time only scalars are sent from the host to the FPGA via PCIe.

A single fully-pipelined point adder on the FPGA which adds points to buckets as directed by a pippenger controller until there are no more points left. Once all points have been added into buckets, the FPGA streams back the result for the host to do the final bucket sum.

This approach allows us to focus on implementing a very high performance adder on the FPGA (as these additions dominate Pippenger’s algorithm), and then leaving smaller tasks for the host to perform.

FPGA Bucket Sum

In our implementation, the meat of the computation is performed by a fully pipelined point adder with a high but static latency (>200 cycles). Naively, if a coefficient needs to be added to a bucket that is currently in use by the point adder we need to wait until the addition is complete before trying again. Waiting 200 clock cycles will severely affect performance. The page about the pippenger controller discusses some tricks to minimize the impact of this.

We utilize a well-known trick to reduce the memory usage by transforming the scalar into signed digit representation for scalars for every bucket.

FPGA Point Adder

The most expensive part of the pipelined point adder computation is field multiplications. Our implementation is based around well-known tricks in barrett reduction.

To reduce the number of field multiplications, we convert the points representation from it’s original Weistrass curve form into a Twisted Edwards curve representation. This reduces the amount of field multiplication substantially. We go one step further to reduce the field multiplication operations with some precomputation tricks in the adder implementation.